Funciones trigonométricas en el plano
cartesiano
Las funciones
trigonométricas en el plano
cartesiano se describen como relaciones entre los lados de un triángulo rectángulo (triángulo
en el cual uno de sus ángulos es recto).
Si el triángulo tiene un ángulo agudo θ se pueden encontrar seis razones
entre las longitudes de los lados a,b y c del triángulo.
b/c, a/c, b/a, a/b, c/a, c/b
Estas relaciones dependen del ángulo θ y no del
tamaño del triángulo. Si dos triángulos tienen ángulos iguales son semejantes y
sus lados son proporcionales.
Las relaciones son funciones de θ y se les llama funciones trigonométricas.
Las funciones trigonométricas son: seno, coseno, tangente, cotangente, secante y cosecante sus símbolos respectivamente son: sen, cos, tan, cot, sec y csc.
Por ejemplo sen θ indica la relación b/c respecto a θ.
Si θ es el ángulo agudo del triángulo rectángulo entonces:
Sen θ = b/c
Cos θ = a/c
Tan θ = b/a
Cot θ = a/b
Sec θ = c/a
Csc θ = c/b
El dominio de cada una de las funciones trigonométricas es el conjunto
de todos los ángulos agudos. Si el ángulo θ es agudo a los lados del triángulo se les llama cateto adyacencente , cateto opuesto e hipotenusa.
Es decir:
Sen θ = c. opuesto/hipotenusa
Cos θ = c. adyacente/hipotenusa
Tan θ = c. opuesto/c. adyacente
Cot θ = c. adyacente/c. opuesto
Sec θ = hipotenusa/c. adyacente
Csc θ = hipotenusa/c. opuesto
Los valores de las seis funciones trigonométricas son positivos para
todo ángulo agudo θ.
Seno y cosecante son recíprocas entre sí.
Coseno y secante son recíprocas entre sí.
Tangente y cotangente son recíprocas entre sí.
Sen θ = 1/csc
Cos θ = 1/sec
Tan θ = 1/cot
Cot θ = 1/tan
Sec θ = 1/cos
Csc θ = 1/sen
EJEMPLO
Si el ángulo θ es agudo y cos θ = 3/5, calcula el valor de las seis
funciones trigonométricas de θ.
Cateto adyacente = 3
Hipotenusa = 5
Aplicando el teorema de Pitágoras :
32 + (c. opuesto)2 = 52
(c. opuesto)2 = 52 – 32
(c. opuesto)2 = 16
Cateto opuesto = 4
Las funciones trigonométricas de este triangulo son las siguientes:
Sen θ = 4/5
Cos θ = 3/5
Tan θ = 4/3
Cot θ = 3/4
Sec θ = 5/3
Csc θ = 5/4
NOTA: Las calculadoras científicas tienen teclas como SIN, COS y TAN que
se pueden usar para calcular los valores de esas funciones, antes de utilizar
la calculadora para determinar los valores de funciones hay que seleccionar el
modo grados o radian según nuestro ángulo.
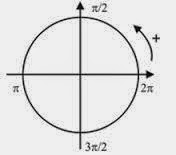
Plano cartesiano :
Al hacer las gráficas de las funciones trigonométricas siempre suponemos
que los ángulos están en radianes.
Ejemplo:
ELI UTC